3D Graphics Beginner

简体中文

English

简体中文

English

Appearance

On this page

3D图形学初学者入门介绍 ​

-- 关于完全能听懂的电脑是怎么把3D游戏画出来的我知道的那些事 ​

引子问题 ​

考虑这样一个引子问题：写一段程序，用来在一张2D画布上依据对一个场景的描述，画出一幅画。你会怎样用编程语言实现它？

让我们提供更多细节并更好地定义我们要解决的问题：

  • 程序输入：对一个场景的描述。一个非常简单的场景描述的例子："一个长宽均为50单位的矩形，位于画面的左上角"
  • 程序输出：一张100x100的2D画布：用像素数组来表示。一个像素代表颜色，它由3个数字（浮点数）组成：红, 绿, 蓝。

最简单的思路下，我们大概会写出像这样的程序（使用Typescript和HTML）

typescript
const c = document.createElement("canvas");
c.width = 100;
c.height = 100;
document.body.appendChild(c);
const ctx = c.getContext("2d");
const imgData = ctx.createImageData(c.width, c.height);
for (let x = 0; x < c.width; x++) {
  for (let y = 0; y < c.height; y++) {
    if (x <= 50 && y <= 50) {
      const i = 4 * (x * c.height + y);
      imgData.data[i + 0] = 255;
      imgData.data[i + 1] = 0;
      imgData.data[i + 2] = 0;
      imgData.data[i + 3] = 255;
    }
  }
}
ctx.putImageData(imgData, 0, 0);

预备技能：熟悉编程语言

你应该能够阅读和理解这段程序，以继续阅读后面的部分。如果你使用过其他编程语言而单纯对Typescript不熟悉，也许你可以看看这篇文章：Tutorials for programmers from other languages

你大约已经发现了，上面这段程序把“场景描述”硬编码到了程序里。这是因为我们只是人工地把自然语言下的“场景描述”写成了程序，它对其他的场景并没有可扩展性。如果我现在给我们之前的“场景描述”加上 "……，和一个蓝色的圆形位于画面的中央" 呢？为了解决这个问题，我们可能想到为我们的场景描述提供更多的数据结构。

typescript
class DrawObject {
  type: 'rect' | 'circle',
  color: number[],
};

class Rect extends DrawObject {
  top: number,
  left: number,
  bottom: number,
  right: number
};

class Circle extends DrawObject {
  x: number,
  y: number,
  radius: number
};

const shapes: DrawObject[];

// ...

但如果说，我想画一辆汽车呢？汽车和矩形、圆形可不一样。我们怎么能精确地描述一辆汽车的外形呢？ 我想画一个人，他的胳膊和腿可以像动画那样动起来的那种？ 又如果我想要的画面里同时有一辆车和一个人呢？我们如何表达人和车的相对位置？如何表达人和车相对画面的位置？

除了形状，再来看看颜色。不同于单色的矩形或圆形，一辆汽车的不同部分会有不同的形状。光滑的金属车身表面并非简单的某一种颜色，它的反射颜色也许取决于它周边的环境。而车玻璃则是透明的，它的颜色取决于它后面东西的颜色。还有光源的问题，一辆车在太阳光下和在紫色聚光灯下呈现的颜色也不同，我们如何在程序中处理这一点呢？

咳咳，一下子问太多问题了。不过稍等，其实我们问的这么多问题，大约都处于计算机图形学要研究和解决的问题的范畴。

简单且笼统地说，图形学就是研究如何用计算机完成这么一个任务：把“场景描述信息”转变成“画面”。

把这个任务再拆分成一些更小的子任务，可以帮助我们发现具体需要解决哪些问题：

  • 如何向计算机精确地描述场景？
    • 场景里有什么“东西”，每个“东西”长什么样子，摆在哪里，表面是什么颜色？
    • 如果用拍电影类比，场景是从哪里，什么角度，用什么镜头拍摄的？
  • 如何把已经精确描述的场景信息，最终转变为屏幕上像素的二维数组？

如何向计算机精确地描述场景？ ​

第一个问题：如何向计算机精确地描述场景里的物体。

你一定听说过“3D模型”这个词。是的，这是目前工业界最常用的解决“如何描述一个物体”的方法。所有物体都是由三角形组成...

如果你将一个.obj 3D模型文件以文本文档的形式打开，你所看到的就只是一长串数字。通常每行以v开头的3个数字表示一个顶点（点）的x、y、z坐标。而每3个顶点表示一个三角形。

v -0.806124 0.440184 0.440084
v -0.737070 -0.000000 0.797186
v -0.612160 -0.000000 0.797185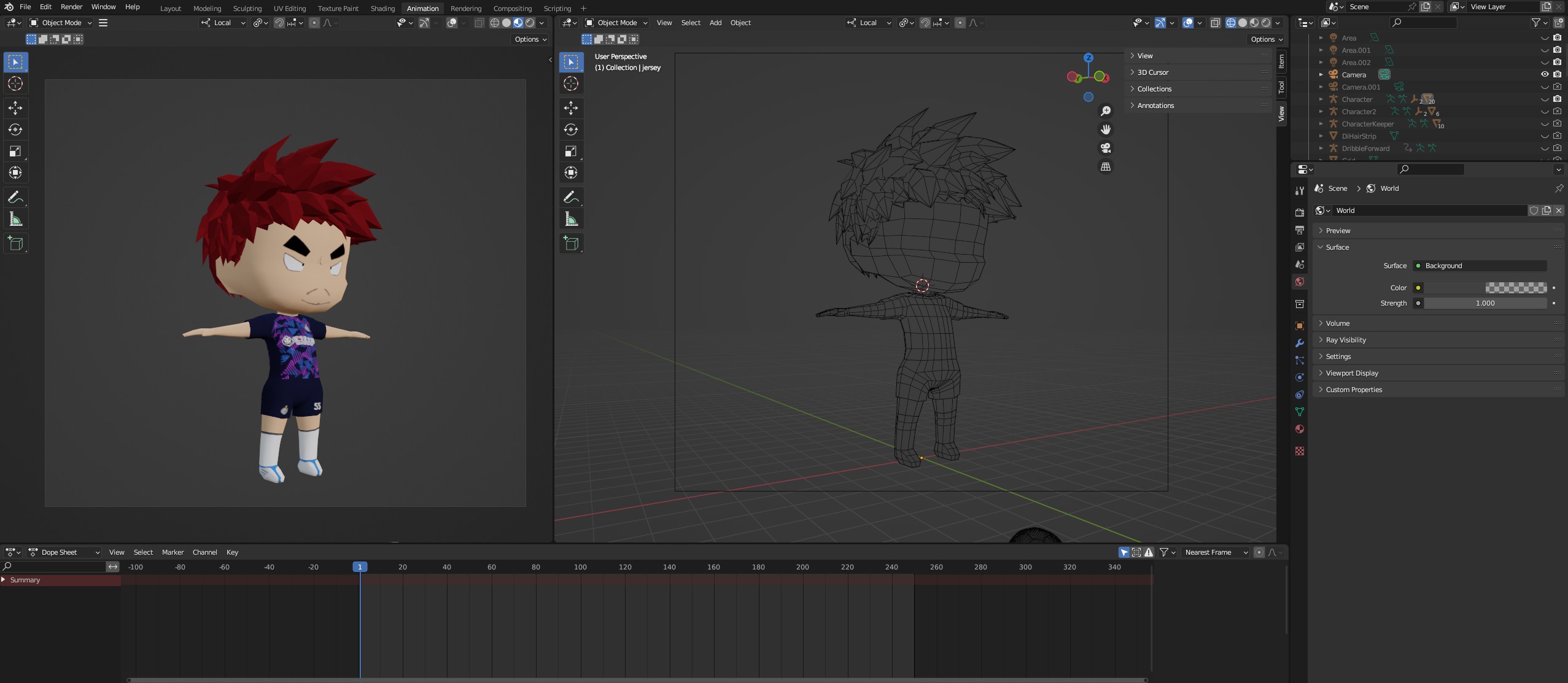
3D建模软件Blender的截图。 从右侧Wireframe视图可以看出，人物模型是由三角形和四边形（两个三角形）构成的。类似的3D建模软件为用户提供了图形化交互界面以方便地创建和调整三角形的顶点位置，并最终导出成保存一系列三角形数据地模型文件，用来被3D渲染程序使用。

于是我们把“画场景”这个问题，转变为了如何“画N个三角形”。也即如何做N次“画一个三角形”这项任务。

为什么是三角形？不是四边形，圆形，或者椭球？

经过历史上的探索，人们发现三角形的应用场景会很普遍，且具有一些良好的性质:

  • 足够简单: 任何三角形都可以通过它的三个顶点坐标来表示。就是三组 (x, y, z)向量, 也即9个浮点数。
  • 三角形中的任意一点，都可由它的三个顶点的线性插值来表示。(因为三角形是凸多边形，四边形不一定是)
  • 多个三角形的组合成或近似组合成其他基本图形（比如四边形可以由两个三角形构成）

所以如果我们的大部分场景中的物体都由三角形构成，那么渲染程序只要解决了“画三角形”这一件事，就可以画出大部分的任意场景。

给定任意已知三个顶点坐标地三角形，如何把它“画”出来？ ​

在之前的画2D圆形的例子中，你所实现的程序实际上是完成一个叫“光栅化”(Rasterization)的步骤：

  • 它的输入：矢量图形信息（一堆三角形的顶点坐标）
  • 它的输出：以二维数组形式排列的像素点颜色值(RGB)
为什么是输出二维数组的像素？

这是由常见图片文件的存储格式（位图）和常用显示设备的成像原理（显示器）所决定。对每一个像素点他们存储红(R)，绿(G)，蓝(B)颜色值，或发射出红(R)，绿(G)，蓝(B)光线。

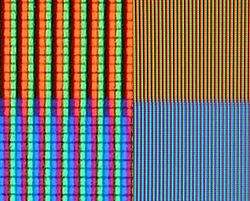
靠近观查显示橙色（上）和蓝色（下）的LCD显示器可以发现每个像素由红绿蓝发光单元组成。

当然，每个像素点存储的数据也可以根据需要而变。比如早期的单色液晶演示器每个像素可能只需要存储一个bit。有些有趣的渲染器也能用ASIIC字符显示每个像素。

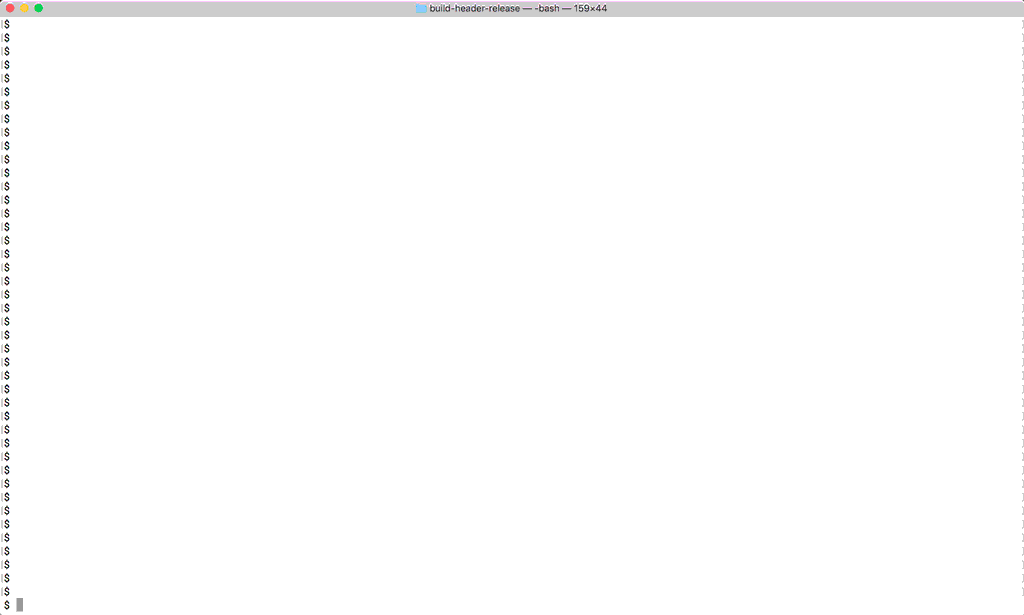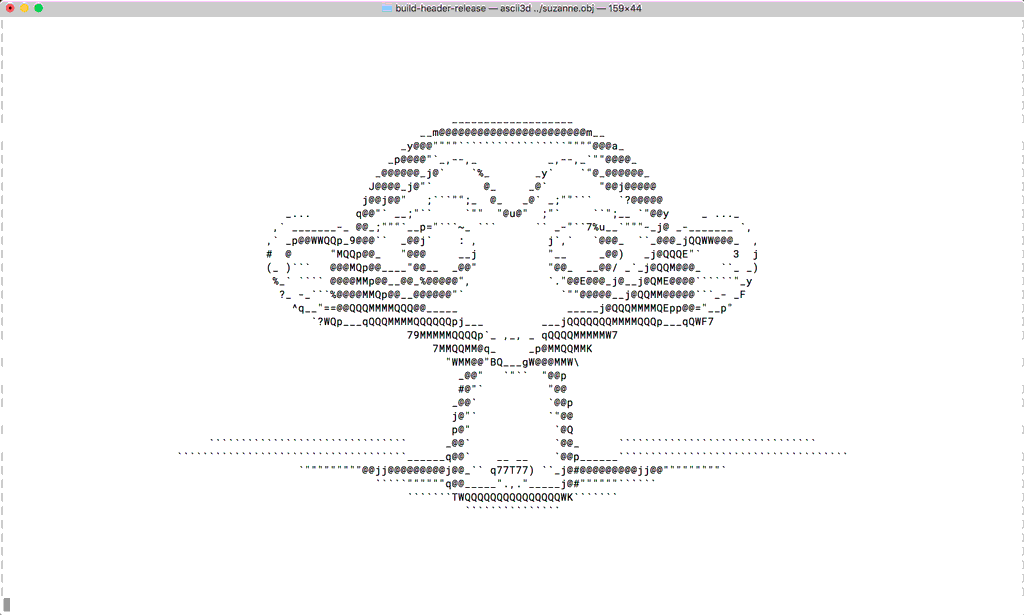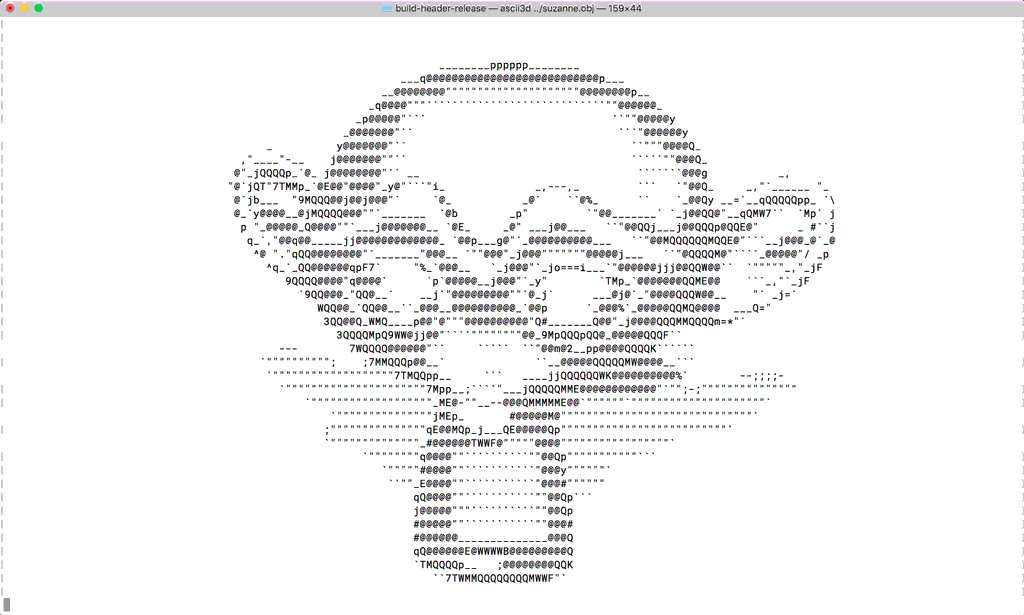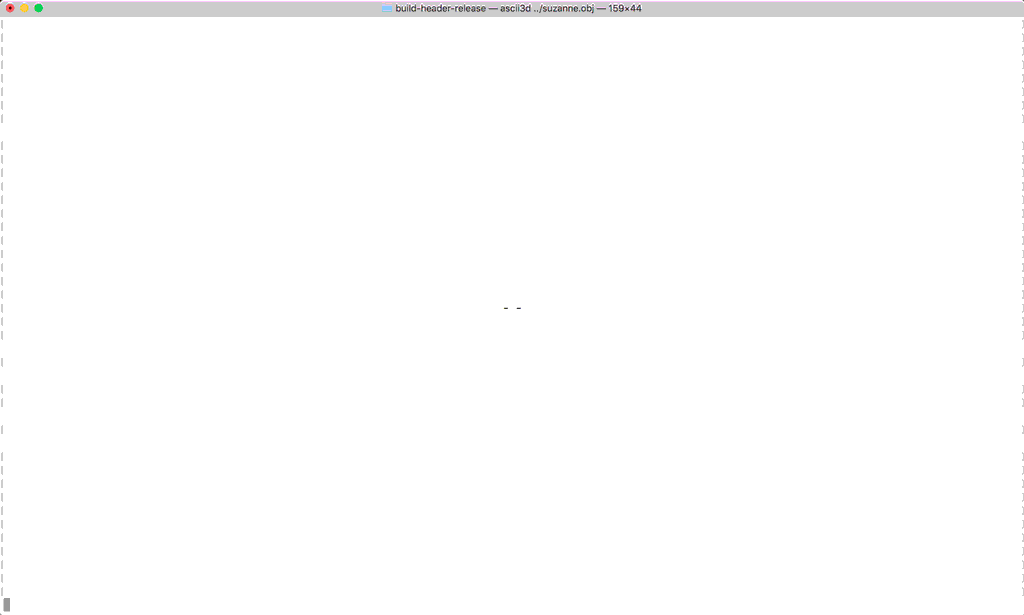
来自github: https://github.com/alecjacobson/ascii3d

在之前的例子中，把一个给定圆心坐标和半径的2D圆形“光栅化”看起来很直接和简单。2D矩形如果和坐标轴对齐（Axis Aligned），也很简单。没对齐的矩形看起来就没那么直接了。还有3D空间中的形状，比如旋转过了的，不正对着画布的三角形“面片”。

对于这些任意摆放的形状，用计算机里分而治之的思想，我们会想到如果我们能把3D空间中任意的图形先处理成“对齐”画布的样子，再去找他们各自覆盖了的像素。我们需要用到一些数学工具来处理“光栅化一个在3D空间中的任意三角形”这项任务。

Vertex Stage里的每个矩阵变换经历的坐标系总览。图片来自 这里

数学：矩阵和变换 ​

如果你学过一点线性代数，你会对这部分概念感到很熟悉。如果你没有学过也没关系，因为我们只会使用一点点最基础的矩阵数学作为工具，只需要了解工具的用途而不必理解工具本身是如何运作的。

我们会把3D空间中的点用齐次坐标(Homogenous coordinate)表示成向量形式

xyz后面的1是干什么的？

这里xyz后面的1仅是用来方便进行平移和投影矩阵运算的。你可以试试用下面平移矩阵T乘上这个向量会得到什么。如果你希望了解更多细节可以阅读仿射变换和齐次坐标

3D空间中的常见变换可以用特定的矩阵表示，比如缩放，旋转（以绕x轴为例），平移分别可以表示为：

用相应的变换矩阵乘以一个点的向量坐标，可以得到这个点变换后的坐标。而一系列变换也可以通过矩阵相乘来叠加。 比如我们如果我们要将一个三角形放大成两倍，绕x轴旋转90度，再沿y轴正向平移3个单位，只需要对这个三角形的三个顶点都依次乘上三个变换矩阵，就能得到这个三角形三个顶点的新坐标了。

坐标系的转换 ​

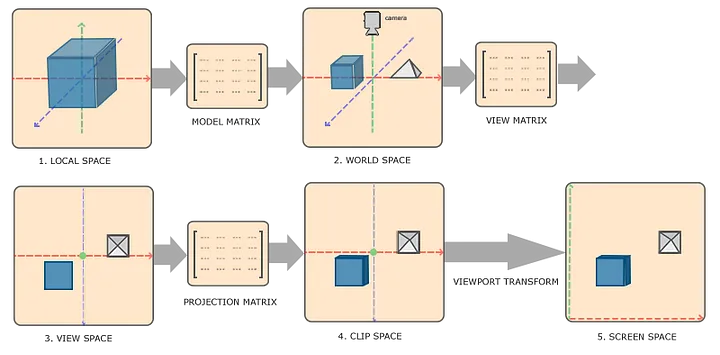
有了上面介绍的数学工具，我们就可以通过变换坐标系来安排和管理场景中来自不同模型的三角形了。很常见的情况是，场景中有多个3D模型。每个3D模型中的三角形的顶点坐标都是在他们各自的坐标系中的。我们首先需要把他们转换到同一个坐标系中，通常称为世界坐标系（World Coordinate）。把各自模型坐标系（Model Coordinate）中的顶点坐标，转换到世界坐标系的变换矩阵，通常叫做模型矩阵（Model Matrix）。它通常可以用一组缩放，旋转，和平移矩阵来表示出来。每个场景中的物体都具有一个模型矩阵，由此我们可以精确地描述每个物体在世界中地摆放情况。

之前介绍了相机的概念。相机/取景框/观察者，和其他物体，3D模型一样，处在世界中。把世界坐标系（World Coordinate）中的顶点坐标，转换到视角所在坐标系（View Coordinate）地变换矩阵，通常叫做视角矩阵（View Matrix）。

投影变换和深度比较：3D→2D的神奇一步 ​

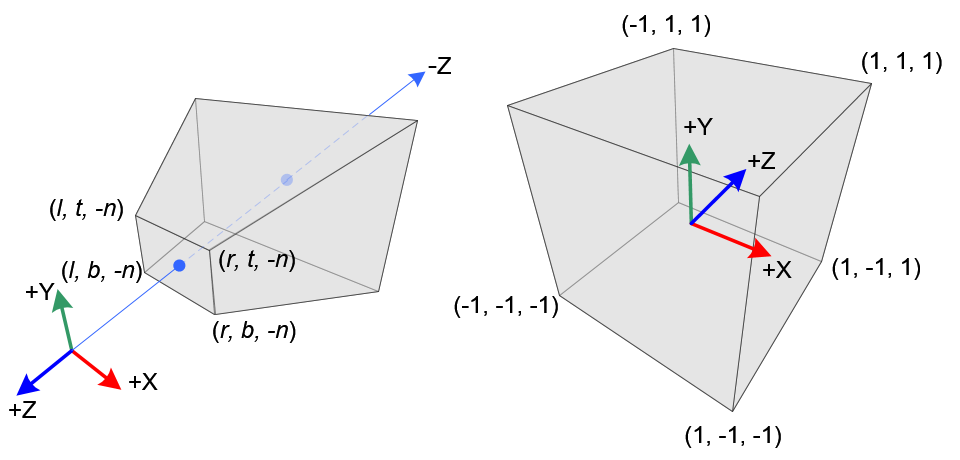
透视投影的视锥（View Frustum），和屏幕所处的标准坐标系（Normalized Device Coordinate）（这里是一个右手系的从-1到1的NDC。其他常用的NDC也有：左手系的从0到1） 图片来自 OpenGL Projection Matrix

到此为止，我们的三角形的顶点坐标经过一些变换，依然处在3D空间内。 现在我们需要把他们从3D空间投影到2D的像素平面上——比如一个原点在画面左下角的坐标系，长宽单位分别对应。我们使用投影矩阵（Projection Matrix）来进行这个坐标变换。它的性质和之前的缩放，旋转，平移矩阵稍有不同（不是仿射矩阵）

投影矩阵具有这样的形式

矩阵里非零的mij由投影相关的参数：如视锥远、近平面距离，视锥角度（Field of view）等导出得到。投影矩阵的重点在于最后一列。我们把它乘上一个向量展开：

我们第一次见到向量w最后一位不为1的情况。如果我们如前约定，向量最后一位w为1时，向量的(x,y,z)表示点的坐标，根据向量的特性我们可以用其除以其最后一位。

我们可以发现在视角坐标系（View Coordinate）中离原点（即相机）越远的点，会因为除以-z，其坐标数值越小。这就是我们在数学上表示出了“近大远小”的透视规律。

经历了这一系列的矩阵变换。我们得到了任意顶点在我们的标准坐标系中的坐标了。（其他仍有一些如视窗变换，将最终坐标的x y单位从比如0~1映射到画布的长宽，在此处省略）

TIP

在这篇介绍概览性文章中我们并未讨论所有关于变换矩阵的细节。有兴趣你可以阅读一系列其他文章WebGPU Fundamentals

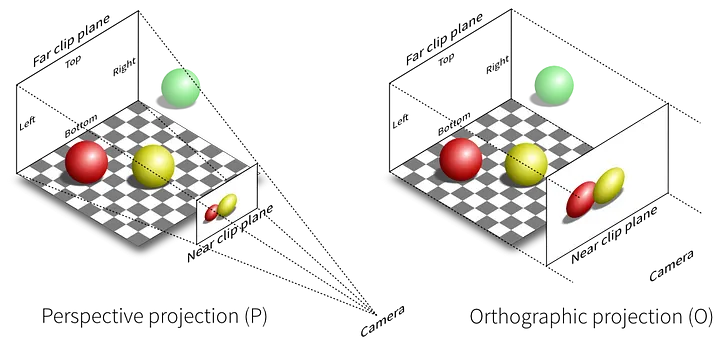
透视投影和平行投影，上述投影矩阵的特征来自透视投影 图片来自 这里

在当今流行的图形API的渲染管线中，以上决定顶点坐标的所有操作，通常被称为顶点渲染阶段（Vertex Stage）。他决定了三角形们的顶点在2D显示框中的坐标。

光栅化 ​

我们刚才这一些操作告诉我们三角形的顶点在屏幕上的坐标。我们还需要把这些三角形的内部“涂满”。在当今流行的图形API中，这一步通常被称为Rasterization Stage。要决定哪些像素落在三角形内部，有不少算法。其中一种被叫做扫描线的算法：我们可以根据三角形的三个顶点，获得其三条边的直线表达式。于是我们可以从三个顶点最小的y轴值开始，对每一个y值，找到x轴值最小的边，和x轴值最大的边。在(xmin, y)和(xmax, y)之间的点，就是我们需要“涂满”的点。

扫描线（Scanline）光栅化的示意图 图片来自 这里

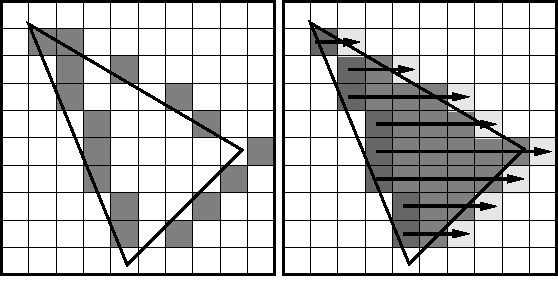
在当今流行的图形API的渲染管线中，光栅化（Rasterization Stage）发生在Vertex Stage之后。且因其通用性，其功能常被内置于硬件驱动中被加速。

图片来自 这里
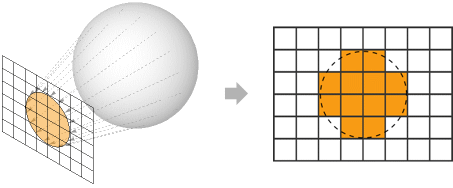
“光栅化”并不是唯一的算法

“光栅化”（Rasterization）仍是当今在实时渲染领域（比如游戏）使用的算法。它很快，有很好的硬件支持，但其实是一种hack——他并没有很好地处理每束光的传播，反射等。同时它也并不是我们解决“把3D世界画出来”这一问题的唯一方案。

“光线追踪”（Ray Tracing ）传统上被广泛应用在离线渲染领域（比如动画电影）。他更善于解决各种来自环境的多次间接反射的光照处理。也因此它通常效果更好但更慢。不过正如你一定听过RTX On，光追等词汇，在硬件性能发展的今天，Ray Tracing也开始被部分运用在实时渲染领域。

在这两者之外，如果感兴趣，你还可以看看Shadertoy，或IQ在bilibili上的介绍视频。这里的程序大多并非用模型文件，而是用Signed Distance Field的数学函数来描述的，配合使用Ray marching方法进行渲染。这在渲染一些无限循环的分形图形，纹理，以及体积云雾等时非常有用。

深度排序 ​

除了“近大远小”，正确的透视还应确保距离近的物体会遮挡住距离远的物体。

渲染一个字母F的3D模型。可以看到模型由多个三角形构成。在3D向2D投影过程中如果我们不注意每个三角形的绘制顺序，会让渲染结果错乱。我们需要保留3D坐标系下顶点到相机的距离信息（z轴，depth），来确保绘制的三角形像素的正确覆盖顺序。图片来自 WebGPU Fundamentals

三角形的像素的离相机的远近距离，其实就是视角坐标系中的z值。如果一个像素被多个（不透明的）三角形涂色，我们只需根据他们的z值排序，选择最近的那个作为像素最终颜色的来源即可。

如何决定每个像素的颜色？ ​

之前的坐标变换和光栅化，让我们可以对任意的三角形，相机位置，投影参数等输入，都可以给出所有三角形顶点在2D屏幕上的坐标，以及每个需要点亮的像素点坐标。

现在，如果我们要画的物体是物理学意义上的绝对黑体，我们已经收工了——只要把每个要画的像素都赋值为RGB=(0, 0, 0)的黑色就行了。

当然，我们要模拟的是真实世界3D渲染，你会发现我们还需要解决的另一个问题：如何决定每个要画的像素的颜色。 其实3D世界中的光影效果的多种多样变化，主要来源于两点：

  • 光源和物体的相对位置
  • 不同物体表面对光的反射，散射，折射等性质的不同

根据物理规律，我们看到的颜色来自于光的颜色（波长），光来自物体表面的反射，而反射光最终来自光源发射出的光子。一个物体的某一点被相机看到而成像，是因为有光线通过了屏幕上的这一像素。这束光线可能是被反射，折射，散射而来。他可能直接来自光源，也可能是被其他表面间接反射。

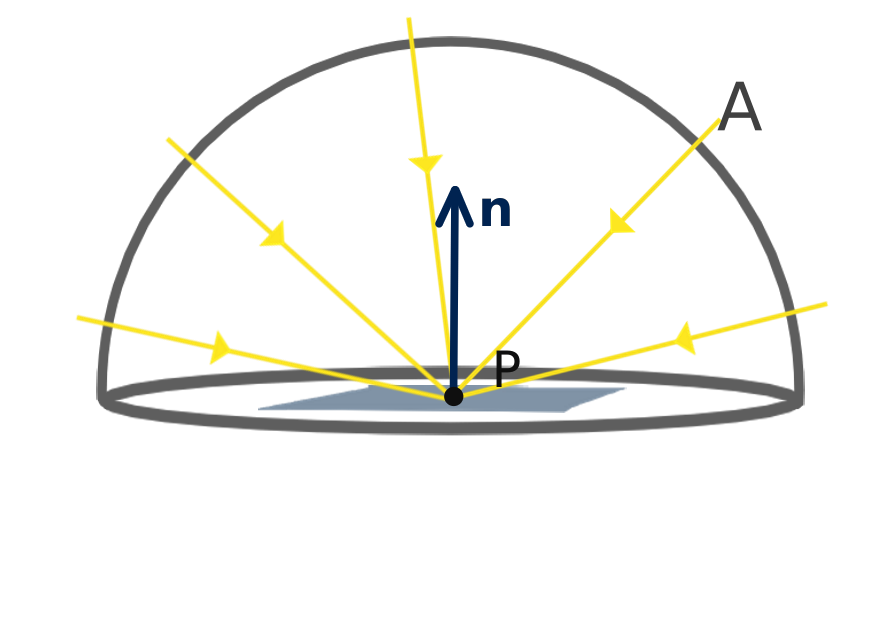
任意一束进入相机的光出射光的颜色和强度，可以表示为所有进入到物体上这一点入射光被反射后的积分。这里的假想的 fr 函数描述了物体在任意给定点，从任意角度的入射光，得到的所有可能反射半球上的反射光的分布，以及它们在颜色和强度上的变化。他模拟了物体表面材料的光学性质。这个函数 fr 叫做双向反射分布函数（BRDF: Bidirectinal Reflectance Distribution Function）。

四种常见表面的 fr 反射光线分布示意图

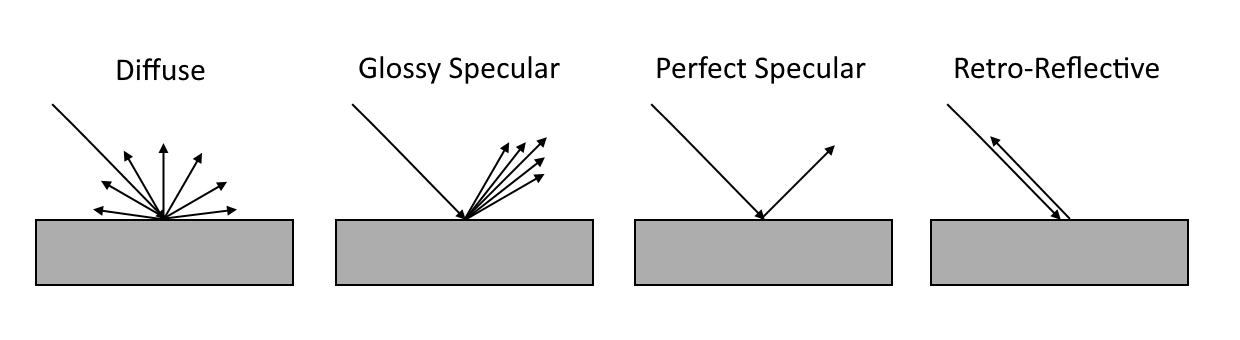
实际使用的算法会根据实际使用需要，对这个理论上的公式进行各种的简化，比如：

  • 只考虑所有入射光线 Li 的一个子集：直接来自光源的入射光。简易而常见的Phong算法的 *fr*即是如此。它使用简单的物体法线向量和直接来自光源的入射光向量的点乘来模拟物体表面的漫反射部分，用物体表面到摄像机的向量和直接来自光源的入射光向量的完美反射向量的点乘来模拟物体表面的镜面部分。
  • 目前很多游戏引擎、通用模型文件常用的基于物理渲染（Physically Based Rendering）的GGX模型可以很好地表示导体和绝缘体的光线表面反射分布

其中F表示Frenel反射（反射光线强度与出射角关系）描述表面的导体/绝缘体反射特性；G表示表面阴影遮挡，D表示法线表面向量分布；它们描述物体表面的光滑/粗糙/坑洼等的特性和程度。

glTF模型选用的PBR光照模型。可以看到不同参数下的物体表面反射特性。
纹理贴图（Texture）

我们之前跳过了如何存储和描述材料的各种反射性质。除了对每种材质（金属，木头）使用一组表示导电性、光滑性、反射参数等数字。纹理贴图是一种广泛常用的方法，能够轻易地给物体上每个点赋予不同的反射数值。还记得三角形的性质吗？其中任意一点都可以表示为它三个顶点的线性插值。如果我们给每个顶点赋予一个贴图坐标，对三角形上每个点的性质，都可以用插值的贴图坐标，到贴图上读取响应的数值来获得。

贴图并可以不局限于物体的表面颜色。常见的其他贴图有法线，材质光滑度，金属度，发光度等。

一个使用各种PBR纹理的头盔模型。可以看到每种功能贴图和最后的渲染效果。sketchfab url
风格化渲染

到此我们讨论的是模拟真实世界照相（Photorealistic）的渲染风格。 实际上我们并非一定要遵循基于真实物理规则渲染。决定每个像素的颜色这一步其实完全取决于你想呈现的画面风格。 3D虚拟世界中物体呈现的颜色不必来自光源和反射，可以像卡通画一样直接指定一种色系，无论它处于何种光源下，也可以给每个物体加上描黑轮廓等等。 我们要做的是写出一段程序，对于任意的顶点和像素位置，能得到统一的风格。

GuiltyGearXrd中的卡通渲染风格。为了渲染效果甚至会调整法线向量以偏移几何意义上的正确值。来自GDC

游戏行业中程序员、技术美术（Techincal Artist）和美术会使用各种办法来达到他们需要的画面和模拟效果。其中很大一部分工作就是写CPU以及GPU程序，配合美术资源，在游戏运行中以能够接受的开销获得各种满意的画面效果

一篇非常有趣的文章：分析游戏GTA5中的渲染流程 article by Adrian Courrèges.
2D渲染

在这套3D渲染管线被广泛使用和被GPU硬件加速的今天，很多2D渲染也是使用的3D渲染技术来实现的。2D场景中的物体常被表示为面向相机的矩形面片。他们上的人物或风景则可以用贴图来表示。有些2D角色的动画也是用一组贴图序列连续播放来实现的。

3D引擎中实现2D游戏，可以看到场景中的前景，后景，人物都是带有贴图的，不同深度的矩形面片

并非局限于游戏。很多窗口GUI，浏览器HTML网页内容元素渲染，看起来和3D无关，但为充分利用这些硬件性能，底层其实都是利用图形渲染API绘制了面片，生成纹理图片的方式来实现的。

在当今流行的图形API中，以上决定像素颜色的所有操作，通常被称为像素渲染阶段（Pixel/Fragment Stage）。他决定了Vertex Stage和Rasterize Stage后产生的像素的颜色。这三个阶段是实时渲染管线中最主要的三个阶段

简化的 GPU API图形渲染管线示意图 from Vulkan Tutorial

讲了这么多，还没提到GPU是干什么的？ ​

我们之前讨论了很多图形学渲染的算法（主要是实时渲染）。你可能会感到困惑，我以前常常听到GPU这个词。可是刚刚所有的算法，似乎都可以用我平时写代码来实现啊，GPU在图形学中扮演了怎样的角色呢？还有，这些渲染算法我用自己已掌握的高级编程语言（如C++，Typescript）都能实现，那我常听说的OpenGL, Direct3D，Vulkan，Metal……又是怎么一回事？

一句话的简短回答：性能！

在实时渲染的三维应用中，为了达到流畅的交互体验，通常至少需要每秒渲染30帧（30fps(frame per second)），甚至60帧（在VR设备中要避免眩晕甚至要达到90帧）。这意味着程序需要在约33毫秒内渲染一帧（60fps的情况下为16.7毫秒）。对于现代游戏而言，这意味着计算机要在这短短的每一帧都需要处理成千上万个三角形和数百万个像素的计算。虽然每个三角形或像素的处理使用的算法都相同，但它们的数据都略有不同（比如入射光的角度，到摄像机的角度等等），使得程序难以将一个像素重复使用计算结果于另一个像素。英语里有个词叫"Embarrasingly Parrallel"。我觉得它十分恰当地描述了这种情况。

传统的CPU结构和计算单元强大，但数量并不多。编写运行在CPU上的程序实现图形渲染算法，不得不顺序地处理所有这些三角形/像素的计算，因而将无法满足实时渲染对计算时间的要求。

历史上，人们观察到这些3D图形应用具有一些共同特征：

  • 对于任何3D游戏/应用程序，每个三角形/像素的计算过程大多是相同且固定的。实际上，与不同、灵活且复杂的CPU程序逻辑相比，这些计算过程相对简单，绝大部分是浮点数的计算。
  • 每个三角形/像素的计算是并行进行的，彼此之间几乎没有依赖关系。即一个像素不需要等待另一个像素的计算结果才能完成自己的计算。

根据这些特性，人们从大约1990年代开始设计专门处理这些任务的硬件，并将其命名为图形处理单元（GPU，Graphics Processing Unit）。如今，GPU由较小的核心和内存缓存组成，与CPU相比较少，但数量众多，这意味着它们可以同时处理许多并行任务。

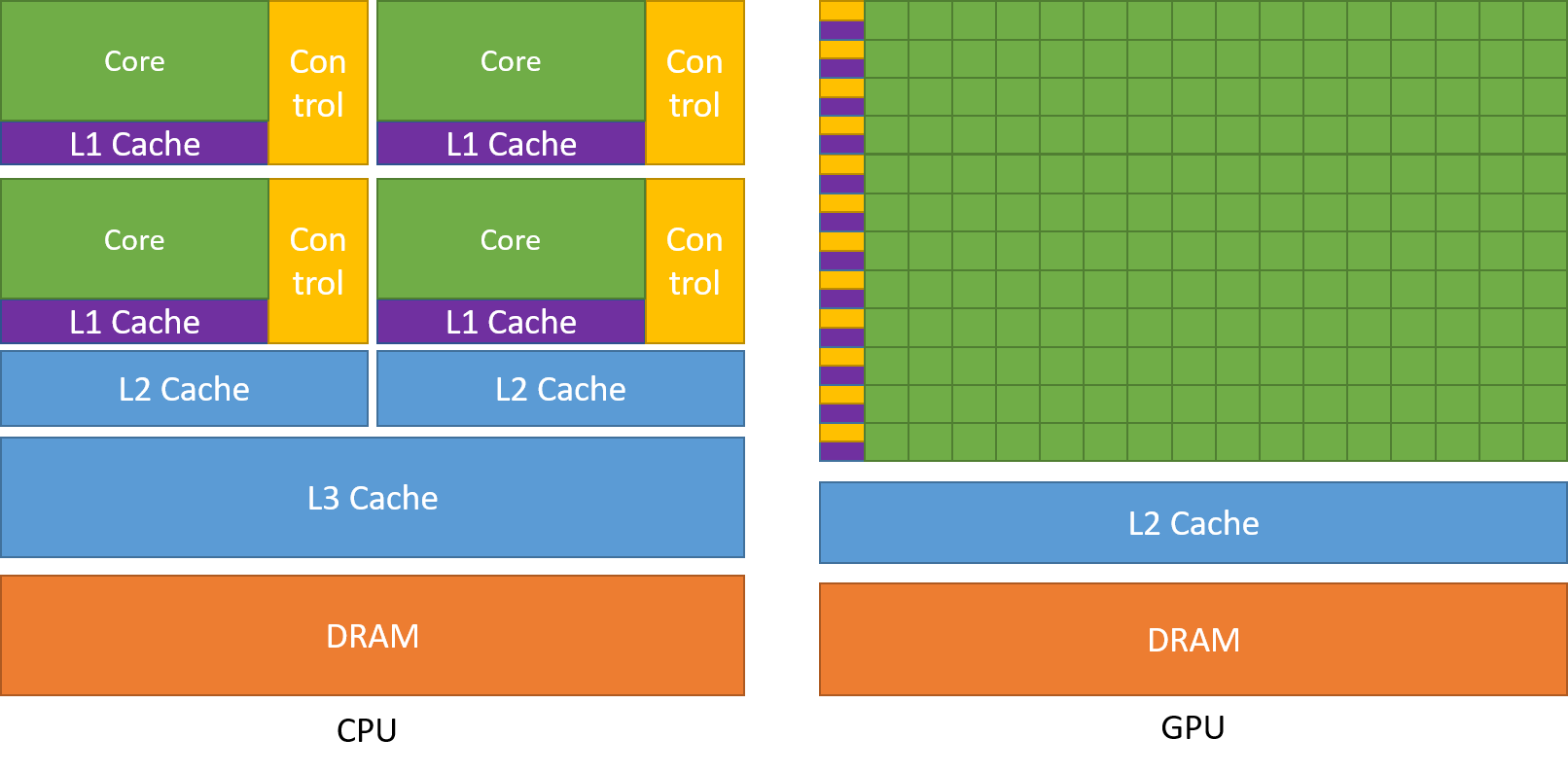
简化的CPU和GPU架构图 Nvidia CUDA programming guide

有了特殊的硬件，封装并抽象其借口，提供常用的图形渲染功能的API也应运而生。OpenGL，Direct3D等就是这样在不同操作系统和平台上方便操纵和使用GPU功能的API。在数十年的发展过程中，他们也从一开始的固定写死渲染管线，仅仅接受提供数据，慢慢演化出了之前对提到过的Vertex Stage，Fragment Stage等阶段进行编程的功能。运行在GPU上的操控Vertex/Fragment Stage的程序，就叫做Shader（着色器/渲染器）。

图形渲染API，Shader，游戏引擎等各自的角色。

图形渲染API（OpenGL Direct3D）常常会提供多种CPU高级编程语言的接口（C++，Java，Javascript） 而Shader，作为运行在GPU有着特定应用场景和功能的程序，通常有自己的编程语言（Shading Langugae），如GLSL（OpenGL），HLSL（Direct3D）等。

图形渲染是常用的游戏引擎（Unity，Unreal）中的一部分功能。游戏引擎封装了图形渲染API的部分（同时也封装了很多其他功能模块如物理模拟，模型预处理，声音处理等），提供给用户更多功能的GUI操作界面和编程接口，让用户集中于游戏内容的开发。使用游戏引擎开发游戏必要时也会编写适应自己需求的Shader。

基于Web的图形渲染API

随着时代发展，在我们的终端设备上进行一些3D渲染已经不再需要下载笨重的客户端程序。即使是Web网页中也有足够强大Javascript API：WebGL和WebGPU。他们不但易于运行（手机，电脑的浏览器点击链接即可），对开发者来说也非常便利（避免许多编译环境的配置），以至于很多Native端的程序也是使用它们来开发的。下面这个canvas的内容就是用WebGPU实时在网页里渲染的

基于Javascript的图形渲染库/引擎也有像Three.js，Babylon.js这样的成熟工具可供选择。

图形渲染API提供的功能，简单来说，就是让开发者方便地根据自身需求完成这两件事情：

  • 把CPU内存里的数据搬运到GPU内存里的Buffer（缓冲区/数据存储区）
  • 告诉GPU怎么操作Buffer里的数据

回想一下我们之前讨论的，把要画的场景描述成三角形顶点坐标：浮点数数组；变换矩阵：浮点数；物体材料的光学反射参数：浮点数；纹理贴图：RGB浮点数数组；……（大多数）图形学领域的数据都被转化成了浮点数。图形渲染API做的就是把这些浮点数搬运到GPU内存，并告诉GPU，每一块数据的意义，和如何读取和使用它们（算法）。

通用GPU编程（GPGPU，General Purpose GPU Programming） ​

GPU诞生之初，正如它名字所指，是用于解决3D图形渲染的问题。不过当你了解了GPU和图形API运作的本质：搬运数据和处理数据，就不难理解，在GPU提供了一种强大的并行计算能力后，会自然被人们发现这种算力在其他领域的作用了。人们也开发了专门用命令GPU处理通用应用领域数据的API（CUDA，OpenCL等）。

Nvidia的CUDA是GPGPU高性能计算常用的API。它被广泛用于机器学习、视频编解码处理、计算金融等很多领域。 Nvidia CUDA programming guide

结语 ​

希望到这里你已经对实时的3D渲染是怎么一回事有了一些概念，不再是两眼一抹黑的状态。

我作为Project driven learning的拥趸，想要提供给你一系列配置好的，可以直接上手直入主题的3D实时渲染相关的Project大作业，让你继续能够练习使用图形学知识完成项目。然而很遗憾这部分工作目前还没有完成，如果你想自己更多探索，也许你可以尝试：

  • webgpufundamentals.org，学习WebGPU API的详细教程。（技能与工业界相关）
  • UCSB GAMES 101，美国大学系统教授图形学知识的课程。（作业内容旨在学习知识算法，并非工业界生产所使用）
  • 直接学习使用Unity, Unreal, Godot等游戏引擎，（或Three.js等渲染库）完成自己想做的项目。